En esta publicación vamos a mostrar cómo se implementaría una de las técnicas más conocidas para reducir el tamaño de una base de datos con variables numéricas en el entorno de Google Cloud, el Análisis de Componentes Principales.
Los Data Scientist estamos acostumbrados a realizar labores de limpieza y preparación de las bases de datos con las que trabajamos, siendo el paso del procesamiento de los datos (o Data Preparation, según la reconocida metodología CRISP-DM) el primordial en cualquier proceso de mundo data.
¿Qué es el Análisis de Componentes Principales?
El Análisis de Componentes Principales (ACP) – o en su versión inglesa, Principal Component Analysis (PCA) – es un método estadístico cuya utilidad radica en la reducción de la dimensionalidad de la base de datos (BDD) con la que estamos trabajando. Esta técnica se utiliza cuando queremos simplificar la base de datos, ya sea para elegir un menor número de predictores para pronosticar una variable objetivo, o para comprender una BDD de una forma más simple.
Este caso sería aplicable para cualquier problema que tengamos con un dataset y se recomendaría analizar las variables disponibles antes de utilizar algoritmos de clustering (Kmeans, jerárquico, DBSCAN…).
La técnica PCA forma parte de los algoritmos de aprendizaje no supervisado de Machine Learning, y se utilizaría solo con aquellas variables numéricas disponibles.
Cómo usar un PCA
Para poder utilizar PCA, se requiere del uso de álgebra lineal, algo que la mayoría de los softwares como R y Python tienen implementado en sus librerías. En el caso que nos ocupa, Google Cloud Platform nos permite realizar PCA en BigQuery mediante unas sencillas consultas gracias a la potencia de BigQuery Machine Learning (Bigquery ML).
Explicación matemática de un Análisis de Componentes Principales
Matemáticamente se necesitarían vectores propios(eigenvectors) y valores propios (eigenvalues) de la matriz de correlaciones o de la matriz de varianzas-covarianzas de las variables. Los eigenvectors de una matriz son todos aquellos vectores que, al multiplicarlos por dicha matriz, resultan en el mismo vector o en un múltiplo entero del mismo. Los eigenvalues son el resultado de multiplicar la matriz por cada eigenvector. En definitiva, a todo eigenvector le corresponde un eigenvalue y viceversa.
Los eigenvalues y el comportamiento de variables
Con los eigenvalues obtendríamos la proporción de varianza explicada por cada Componente. Sabiendo que la suma de los eigenvalues es el total de varianza explicada, se busca siempre maximizar este % con la suma de los componentes. Es importante que en este proceso se seleccionen solo aquellos componentes qué más aporten al total de varianza explicada. Normalmente se aconseja llegar al menos al 80% del total de varianza explicada. Llegar al 80% significa reducción de dimensionalidad y del conjunto de datos original.
Con los eigenvectors analizaríamos cómo se comportan las variables en los distintos componentes y aportariamos una definición a los mismos. Cabe decir que la definición de los componentes en base a los eigenvectors se vuelve más difícil cuanto menores son los eigenvalues, es decir, cuanto menos explique el componente concreto.
¿Cómo se implementa PCA en Google BigQuery?
Para llevar a cabo este experimento en Google Cloud, se ha utilizado el proyecto de BigQuery gratuito bigquery-public-data, del cual hemos utilizado la tabla natality perteneciente al dataset samples.
Disponibilidad del dato
La tabla natality contiene las características de una gran cantidad de nacimientos, combinando variables continuas (año, peso, edad de los progenitores…) y variables discretas (ubicación, raza del bebé y los padres…)
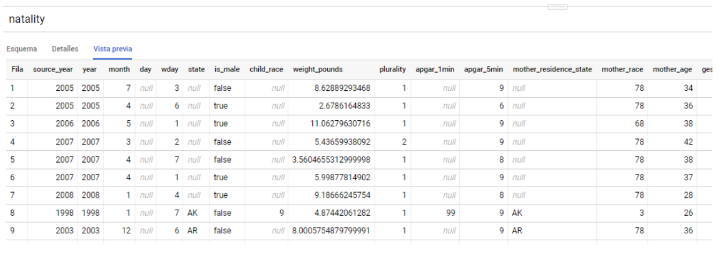
Supongamos que nuestro objetivo es determinar si el sexo del recién nacido (variable is_male) viene motivado por alguna causa explicable con los datos disponibles.
Planteamos que el sexo depende de la edad de los padres, el peso, las semanas de gestación y los hijos totales de la madre. Para ello vamos a crear una tabla ad hoc con estas variables en nuestro dataset de pruebas:
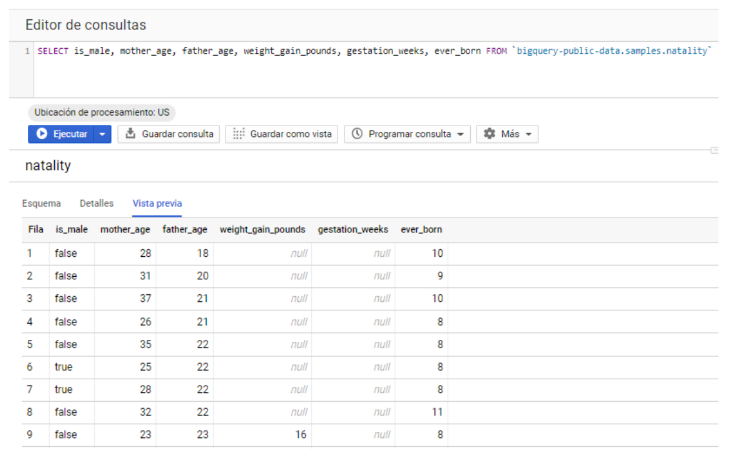
Obsérvese que, como en cualquier caso real, tenemos variables con más de una celda en NULL.
Creación del modelo de Análisis de Componentes Principales
Una vez que tengamos el dataset listo, el siguiente paso será realizar el PCA. El algoritmo, como es del tipo unsupervised learning, necesitará de sus propios datos para darnos los resultados. Es esencial excluir la variable objetivo (endógena), is_male, por dos motivos: es de tipo factor, por lo que no podría aplicársele PCA, y además, por ser la variable objeto de estudio. No hay que olvidar que el objetivo es reducir la dimensionalidad de las variables explicativas, no tocaríamos la dependiente, la target que querremos predecir.
Con la diferencia clara entre target y features , para extraer el conocimiento con PCA solo requerimos de unas simples queries que aprovechan la potencia de BigQuery ML como la que tenemos a continuación:
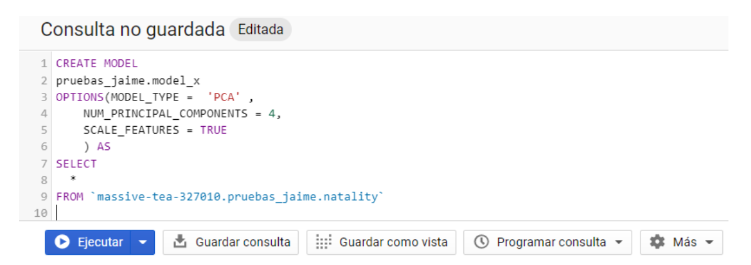
Análisis Query del PCA
Nombrar modelo
Lo primero que debemos hacer es nombrar el modelo en el dataset en el que queremos que este se localice, para ello sigue el esquema dataset.modelo tras el comando CREATE MODEL.
Tipo de modelo
Como segundo paso, habría que incluir las opciones del modelo usando la función OPTIONS(), donde figurarán el tipo de modelo (MODEL_TYPE), que deberá tener el valor ‘PCA’ y el número de componentes principales (NUM_PRINCIPAL_COMPONENTS), que será un número discrecional en función de cuánto nos interese buscar para hacer más o menos sencillo nuestro posterior análisis y reducción de la base de datos.
- En caso de no especificarse, nos daría todos los componentes hasta alcanzar el 100% de varianza explicada. Además, se han incluido las opciones SCALE_FETURES=TRUE, que impone un escalado de las variables para que no haya diferencias entre ellas por las magnitudes utilizadas.
- Elegir la opción PCA_EXPLAINED_VARIANCE_RATIO (si no incluyéramos NUM_PRINCIPAL_COMPONENTS). Esta ratio debe especificar un número entre 0 y 1 para definir hasta qué porcentaje de varianza explicada estamos dispuestos a tener en cuenta.
Resultados
Como resultado se muestran los 4 primeros componentes de la varianza explicada seguidamente tenemos dos opciones cotejar con los componentes o realizar cambios en el PCA.
Resultados del Análisis de Componentes Principales
Con el modelo entrenado, lo primero que podemos hacer para entender mejor nuestros datos con el PCA resultante sería ver cuánta proporción de la varianza nos explican los componentes que hemos obtenido, lo haremos con la función ML.PRINCIPAL_COMPONENT_INFO:
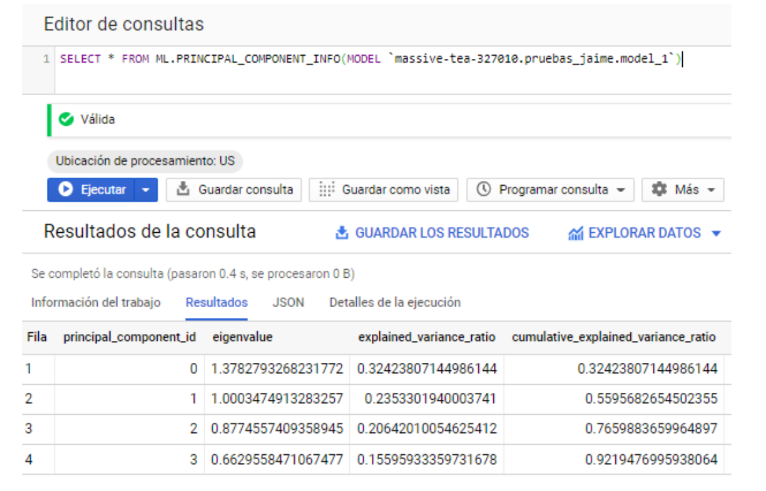
Con esta salida podemos observar los valores propios de cada componente y cuánto representan del total (es decir, qué tan importantes son). Está claro que deberíamos quedarnos con las 3 primeras Componentes (0,1 y 2), y dejaríamos la cuarta en duda, porque sin ella nos acercamos ya bastante a ese 80% ideal. Gráficamente lo podemos ver en Google Data Studio:
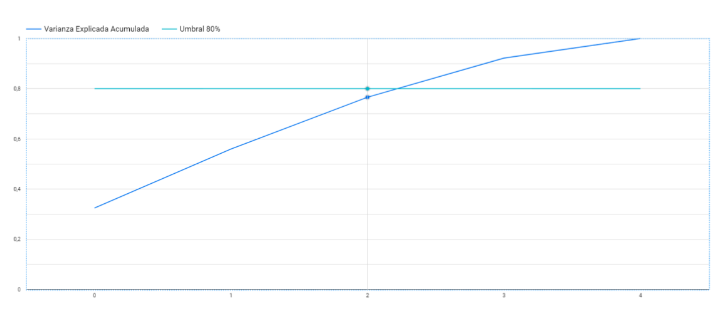
Revisión de valores numéricos
El próximo paso sería la revisión de los valores numéricos asociados a cada variable dentro cada Componente Principal. Esto se consigue con la función ML.PRINCIPAL_COMPONENTS().
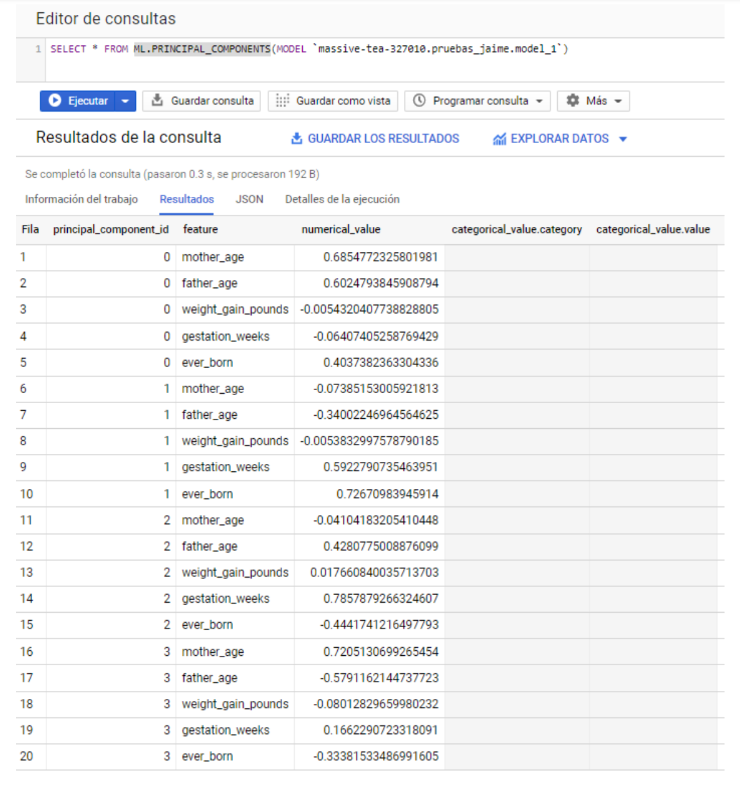
Para la interpretación de estos resultados, deberíamos de fijarnos en los valores numéricos de las variables. Su signo nos indicaría la fuerza relacionada en un mismo sentido, no significa que algo sea más positivo o negativo. De hecho, podría multiplicarse todo por (-1) y se interpretaría del mismo modo.
De esta manera, podríamos decir que la primera (0) Componente está relacionada con el tiempo, pues parece que en ella tienen peso la edad de los padres y el número de hijos totales. Entendemos que el número de hijos totales depende de la edad, a más años más hijos, así que utilizaríamos la proxy del marco temporal para definir la Componente 0.
La siguiente componente (1) da mucho peso a los hijos totales y a las semanas de gestación, contraponiéndolo a la edad del padre; en este caso esta componente podría relacionarse con la fertilidad de la madre.
La componente (2) relaciona las semanas de gestación con la edad del padre, relacionándose estas inversamente con los hijos totales, suponemos varones con edad avanzada y pocos hijos.
La último componente (3) parece que haría referencia a parejas con diferencias en la edad y quizás con pocos hijos.
Conclusión: ¿Qué aporte de valor hemos obtenido?
En este artículo hemos visto como entrenar un modelo PCA a un conjunto de datos de juguete, con todo, podemos resumir la utilidad para un data scientist del PCA:
Selección de variable original
Seleccionar solo algunas variables originales implicadas en los componentes por considerarlas relevantes. Tendríamos un marco de referencia para decidir que features son más importantes.
Selección de variable explicativa
Adjuntar las componentes a la base de datos con ML.PREDICT() y utilizar estas como variable explicativa en lugar de las variables originales.
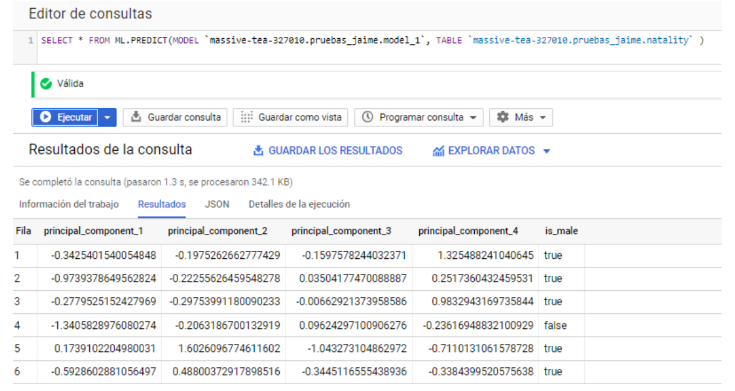
Selección de variables explicativas y originales
Como se ha visto, método PCA es muy sencillo de aplicar en BigQuery, siendo útil cuando tenemos una gran cantidad de datos y manejamos bien el lenguaje SQL. En el caso de que deseemos profundizar aún más en la reducción de la dimensionalidad, recomendaríamos utilizar otros lenguajes como R o Python. Esto nos abriría posibilidades como elegir si trabajamos con la matriz de correlaciones o la matriz de covarianzas, para comparar distintas técnicas. Estos leguajes dan la opción de realizar otros tipos de análisis de reducción de la dimensionalidad como el análisis factorial.
En Hiberus contamos con una unidad especializada en servicios de Data & Analytics formada por un equipo de profesionales con amplio expertise en en tecnología, análisis de datos e innovación. Somos expertos en Big Data, Machine Learning, Business Intelligence 2.0, y Business Intelligence y Analytics tradicional. Descubre todo lo que podemos hacer por ti.
¿Quieres más información sobre nuestros servicios de Data & Analytics?
Contacta con nuestro equipo de expertos en Data & Analytics



