En el mundo tecnológico actual, donde la eficiencia y la precisión son cada vez más esenciales, las matemáticas emergen como una herramienta para la optimización de proyectos. Por tanto, desde el departamento de IA y data de hiberus buscamos cómo implementar técnicas matemáticas para encontrar soluciones óptimas a desafíos complejos. En este artículo, nos centraremos en particular, en una rama de la matemática aplicada, la investigación operativa y los problemas de optimización.
¿Qué es la investigación operativa?
La investigación operativa es una rama de la matemática aplicada centrada en el estudio de métodos matemáticos que permiten ayudar en la resolución de problemas y la toma de decisiones a través del análisis de los datos disponibles de un problema.
Dentro de la investigación operativa existen tres principales vertientes: simulación, optimización y probabilidad y estadística.
- La simulación se centra en la construcción de modelos que permiten replicar o simular posibles escenarios. Así, se puede determinar cuál es la mejor opción sin necesidad de implementar todas. Por ejemplo, la simulación de tratamientos médicos para determinar cuál puede ser el más eficaz según el historial del paciente.
- La probabilidad y la estadística permiten, a partir de unos datos, sacar relaciones entre ellos para realizar inferencias y predicciones. Por ejemplo, para predecir tendencias o sacar correlaciones en los datos.
- Finalmente, la optimización se centra en la búsqueda de la mejor solución dados un objetivo y unas restricciones. Este enfoque abarca una variedad de aplicaciones, desde la planificación de rutas hasta la asignación eficiente de recursos.

Estos modelos permiten una resolución eficaz, rápida y objetiva de problemas con una función objetivo concreta.
Aplicaciones de la Investigación operativa: Optimización matemática
En este artículo nos vamos a centrar en esta última vertiente, donde hiberus ya ha participado en varias soluciones. En primer lugar, expondremos brevemente algunos casos de éxito.
Asignación de horarios
La primera aplicación de modelos de optimización fue para elaborar un calendario laboral, determinando los días de trabajo y descanso de los empleados. Esta aplicación ha reducido significativamente la carga de trabajo asociada con la generación de estos calendarios, ya que implica asegurar el cumplimiento de ciertas condiciones específicas.
Asignación de quirófanos
Otro caso de éxito ha sido la aplicación de modelos de optimización en el sector médico. En este caso, el objetivo del modelo era reducir el tiempo de espera medio en la lista de espera. Así, en un primer lugar el modelo determinaba cuántas horas asignar a cada especialidad médica y, a continuación, distribuía las operaciones correspondientes en esos rangos de tiempo.
Planificación de campañas de plantación
Por último, se aplicó un modelo de optimización para la planificación de campañas de plantación. En este caso, a partir de unos modelos de Machine Learning previamente entrenados, el objetivo consistía en establecer la cantidad óptima a plantar semanalmente para asegurar el cumplimiento de la demanda de la campaña y minimizar las pérdidas de plantas.
Etapas de un modelo de investigación operativa
Pero ¿qué proceso debemos seguir para llegar a elaborar e implementar un modelo?
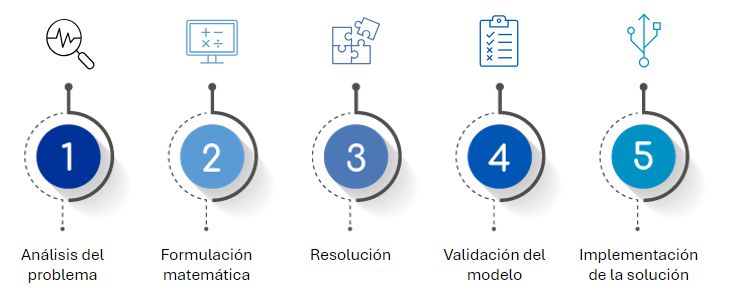
- En primer lugar, es importante realizar un buen análisis del problema, es decir, identificar y definir los objetivos, variables y restricciones del problema.
- Una vez se ha formulado el problema, hay que definir un modelo matemático que lo represente y permita su resolución.
- Después, teniendo en cuenta el modelo matemático, se debe decidir qué método de resolución es el más apropiado para resolver el problema.
- Tras la resolución del problema se debe validar el modelo, es decir, que la solución devuelta sea factible y, por tanto, el modelo funciona correctamente.
- Finalmente, una vez se ha obtenido un modelo efectivo, es posible implementar la solución en el mercado.
Tipos de problemas de investigación operativa
Los modelos se clasifican según el tipo de variable y según la naturaleza de la función objetivo y las restricciones.
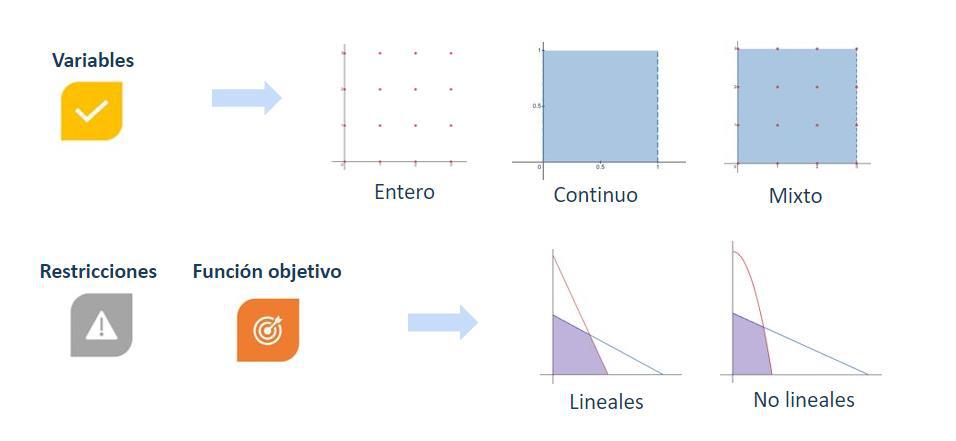
Según el tipo de variable distinguimos entre:
- Problemas enteros: con todas las variables binarias o enteras, como podría ser el número de productos a fabricar.
- Problemas continuos: donde todas las variables son continuas. Por ejemplo, el coste de fabricación de un producto.
- Problemas mixtos: aquellos que poseen tanto variables continuas como enteras.
Por otro lado, según la naturaleza de la función objetivo y de las restricciones se clasifica en:
- Problemas lineales: todas las funciones objetivo y restricciones son lineales
- Problemas no lineales: en otro caso
Métodos de resolución
Para finalizar, hablaremos sobre los distintos métodos de resolución de un problema de optimización. Estos métodos se dividen en dos categorías: exactos y aproximados.
Los métodos exactos son aquellos que siempre devuelven la solución óptima al problema. Por tanto, un modelo de optimización se resolverá idealmente con métodos exactos. Sin embargo, esto no siempre es posible. Ya sea porque la dimensión del problema es demasiado grande, lo que incurre en un tiempo de resolución alto; o porque las restricciones complican excesivamente el problema, y el método exacto ni siquiera es capaz de resolverlo.
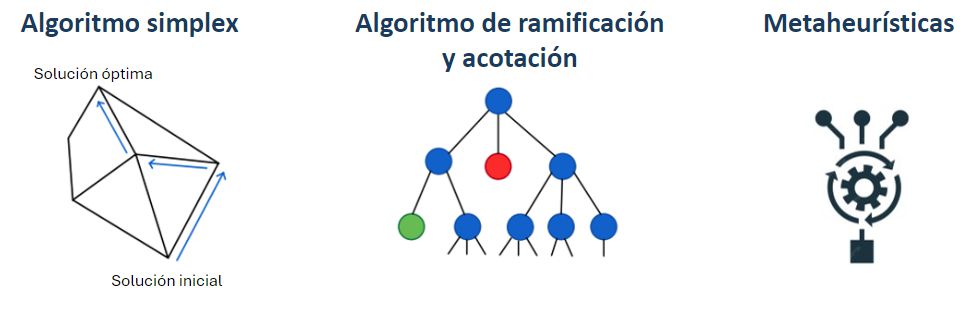
Será en estos casos cuando se apliquen métodos aproximados. El enfoque más común es el empleo de metaheurísticas, modelos que, a partir de una solución inicial y otros algoritmos ya definidos, como el genético, van aproximándose hacia la solución óptima hasta que se cumpla un criterio de terminación.
Algunos ejemplos de algoritmos exactos que se pueden emplear son el algoritmo simplex para modelos continuos y el algoritmo de ramificación y acotación para modelos enteros o mixtos.
Ejemplo práctico de investigación operativa
Para terminar, explicaremos como resolver un problema sencillo de asignación de recursos con la librería de optimización de Google OR Tools. Comenzamos instalando la librería e importando el modelo que vamos a emplear para resolver el problema

Supongamos que queremos modelar y plantear el siguiente problema:
Una compañía produce escritorios, mesas y sillas. La fabricación de cada unidad de uno de estos muebles precisa madera y dos tipos de mano de obra: acabado y carpintería. La cantidad de cada recurso necesaria para fabricar una unidad y el beneficio son los siguientes:
| Escritorio | Mesas | Sillas | Disponibilidad | |
| Madera (unidades) | 8 | 6 | 1 | 48 |
| Acabado (horas) | 4 | 2 | 1,5 | 20 |
| Carpintería (horas) | 2 | 1,5 | 0,5 | 8 |
| Beneficio (euros) | 60 | 30 | 20 |
|
¿Cómo debe organizar la compañía la producción para maximizar los beneficios?
En primer lugar, definimos las variables. En este caso, serán la cantidad de escritorios, mesas y sillas a producir respectivamente. Por tanto, serán variables enteras.

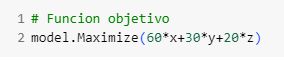
Así, una vez hemos definido las variables, podemos formular la función objetivo y las restricciones. Como el objetivo del problema es maximizar los beneficios, la función objetivo es: 60x+30y+20z
Por otro lado, las restricciones considerarán que no se excedan las unidades u horas disponibles para la fabricación de los productos. Por tanto, las restricciones serán las siguientes:
- Madera: 8x+6y+z ≤ 48
- Acabado: 4x+2y+1.5z ≤ 20
- Carpintería: 2x+1.5y+0.5z ≤ 8

Finalmente, una vez se ha planteado el problema, basta con llamar al solucionador para obtener la solución óptima:
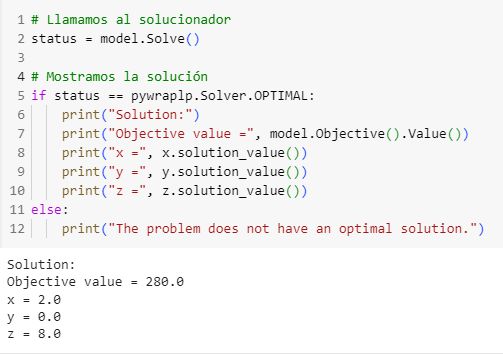
Por tanto, para maximizar los beneficios, se deben fabricar dos escritorios y ocho sillas, obteniendo un beneficio de 280 euros.
En hiberus contamos con una unidad especializada en servicios de Data & Analytics formada por un equipo de expertos en Big Data, Machine Learning, IA, Gobierno de Datos, Business Intelligence y Analytics, entre otras tecnologías. ¿Necesitas una solución basada en tecnología de datos? ¡Contacta con nosotros y estaremos encantados de ayudarte?
¿Quieres más información sobre nuestros servicios de Data & Analytics?
Contacta con nuestro equipo de expertos en Data & Analytics